万人模考数学一/三

类型：试卷工厂

题数：32

总分：223.0分

开始考试

单选题（每小题4分，数一同学完成：1、2、3、4、5、6、7、8题。数三同学完成：1、2、3、5、6、7、9、10题。）

若实数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>$ 满足 $<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mrow><mi>l</mi><mi>i</mi><mi>m</mi></mrow><mrow><mi>x</mi><mo>→</mo><mn>1</mn></mrow></munder><mfrac><mrow><mn>2</mn><msup><mfenced><mrow><mi>x</mi><mo>-</mo><mn>1</mn></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced><mrow><mi>x</mi><mo>-</mo><mn>1</mn></mrow></mfenced><mn>3</mn></msup></mrow><msup><mfenced><mrow><mi>ln</mi><mi>x</mi></mrow></mfenced><mi>n</mi></msup></mfrac><mo>=</mo><mfrac><mn>1</mn><mi>a</mi></mfrac><mi></mi></math>$ ，则

A

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mi>a</mi><mo>=</mo><mn>2</mn></math>$

B

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo>=</mo><mn>1</mn><mo>,</mo><mi>a</mi><mo>=</mo><mn>1</mn><mi></mi></math>$

C

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo>=</mo><mn>2</mn><mo>,</mo><mi>a</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi></mi></math>$

D

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo>=</mo><mn>1</mn><mo>,</mo><mi>a</mi><mo>=</mo><mn>2</mn></math>$

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><munder><mrow><mi>l</mi><mi>i</mi><mi>m</mi></mrow><mrow><mi>n</mi><mo>→</mo><mo>∞</mo></mrow></munder><mroot><mrow><mn>1</mn><mo>+</mo><msup><mfenced open="|" close="|"><mi>x</mi></mfenced><mi>n</mi></msup><mo>+</mo><msup><mi>e</mi><mrow><mi>n</mi><mi>x</mi></mrow></msup></mrow><mi>n</mi></mroot></math>$ 不可导点的个数为

A

0个

B

1个

C

2个

D

3个

设 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><msubsup><mo>∫</mo><mi>x</mi><mrow><mi>x</mi><mo>+</mo><mfrac><mi mathvariant="normal">π</mi><mn>2</mn></mfrac></mrow></msubsup><mfenced open="|" close="|"><mrow><mi>sin</mi><mi>t</mi></mrow></mfenced><mi>d</mi><mi>t</mi></math>$ ，则

A

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mi mathvariant="normal">π</mi></mrow></mfenced></math>$

B

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>></mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mi mathvariant="normal">π</mi></mrow></mfenced><mi></mi></math>$

C

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo><</mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mi mathvariant="normal">π</mi></mrow></mfenced></math>$

D

当 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>></mo><mn>0</mn></math>$ 时 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>></mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mi mathvariant="normal">π</mi></mrow></mfenced></math>$ ，当 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo><</mo><mn>0</mn></math>$ 时 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo><</mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mi mathvariant="normal">π</mi></mrow></mfenced></math>$

设球面 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>S</mi><mo>:</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><msup><mi>z</mi><mn>2</mn></msup><mo>=</mo><msup><mi>R</mi><mn>2</mn></msup></math>$ ，在下列四组积分中，同一组的两个积分均为零的是

A

$<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mo>∬</mo><mi>S</mi></munder><msup><mi>x</mi><mn>2</mn></msup><mi>d</mi><mi>S</mi><mo>,</mo><munder><mo>∬</mo><mi>S</mi></munder><msup><mi>x</mi><mn>2</mn></msup><mi>d</mi><mi>y</mi><mi>d</mi><mi>z</mi></math>$

B

$<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mo>∬</mo><mi>S</mi></munder><mi>x</mi><mi>d</mi><mi>S</mi><mo>,</mo><munder><mo>∬</mo><mi>S</mi></munder><msup><mi>x</mi><mn>2</mn></msup><mi>d</mi><mi>y</mi><mi>d</mi><mi>z</mi><mi></mi></math>$

C

$<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mo>∬</mo><mi>S</mi></munder><mi>x</mi><mi>d</mi><mi>S</mi><mo>,</mo><munder><mo>∬</mo><mi>S</mi></munder><mi>x</mi><mi>d</mi><mi>y</mi><mi>d</mi><mi>z</mi><mi></mi></math>$

D

$<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mo>∬</mo><mi>S</mi></munder><mi>x</mi><mi>y</mi><mi>d</mi><mi>S</mi><mo>,</mo><munder><mo>∬</mo><mi>S</mi></munder><mi>y</mi><mi>d</mi><mi>z</mi><mi>d</mi><mi>x</mi><mi></mi></math>$

满足n元线性方程组 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>x</mi><mo>=</mo><mi>b</mi></math>$ 有唯一解的充要条件个数为
①A为可逆矩阵；
②齐次线性方程组 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>x</mi><mo>=</mo><mn>0</mn></math>$ 只有零解；
③A的行向量组线性无关；
④矩阵A的列向量组线性无关，且向量b可由A的列向量组线性表示。

A

1个

B

2个

C

3个

D

4个

设 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>1</mn></msub><mo>=</mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mo>-</mo><mn>2</mn></mtd><mtd><mn>3</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>2</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>3</mn></mtd></mtr><mtr><mtd><mn>3</mn></mtd><mtd><mn>3</mn></mtd><mtd><mn>3</mn></mtd></mtr></mtable></mfenced></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>2</mn></msub><mo>=</mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>2</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>3</mn></mtd><mtd><mn>3</mn></mtd><mtd><mn>3</mn></mtd></mtr></mtable></mfenced><mi></mi></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>3</mn></msub><mo>=</mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>2</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>2</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>3</mn></mtd><mtd><mn>3</mn></mtd><mtd><mn>2</mn></mtd></mtr></mtable></mfenced><mi></mi></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>4</mn></msub><mo>=</mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>2</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>3</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>3</mn></mtd><mtd><mn>2</mn></mtd><mtd><mn>2</mn></mtd></mtr></mtable></mfenced><mi></mi></math>$ ，则 $<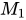math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>1</mn></msub><mi></mi></math>$ ， $<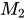math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>2</mn></msub><mi></mi></math>$ ， $<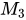math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>3</mn></msub><mi></mi></math>$ ， $<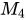math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>4</mn></msub><mi></mi></math>$ 中不能与对角阵相似的是

A

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>1</mn></msub></math>$

B

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>2</mn></msub><mi></mi></math>$

C

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>3</mn></msub><mi></mi></math>$

D

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>M</mi><mn>4</mn></msub><mi></mi></math>$

设随机变量X，Y的数学期望分别为-2，2，方差分别为1和4，相关系数为-0.5，则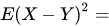 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><msup><mfenced><mrow><mi>X</mi><mo>-</mo><mi>Y</mi></mrow></mfenced><mn>2</mn></msup><mo>=</mo></math>$

A

11

B

23

C

30

D

55

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>X</mi><mo>~</mo><mi>N</mi><mfenced><mrow><mi>μ</mi><mo>,</mo><msup><mi>σ</mi><mn>2</mn></msup></mrow></mfenced></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>σ</mi><mn>2</mn></msup></math>$ 未知， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>X</mi><mn>1</mn></msub><mo>,</mo><mo>⋯</mo><mo>,</mo><msub><mi>X</mi><mi>n</mi></msub></math>$ 为来自 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>X</mi></math>$ 的样本值，现对 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>μ</mi></math>$ 进行假设检验。若在显著性水平 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi><mo>=</mo><mn>0</mn><mo>.</mo><mn>05</mn></math>$ 下拒绝了 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>H</mi><mn>0</mn></msub><mo>:</mo><mi>μ</mi><mo>=</mo><msub><mi>μ</mi><mn>0</mn></msub></math>$ ，则当显著性水平 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi><mo>=</mo><mn>0</mn><mo>.</mo><mn>08</mn></math>$ 时，下列结论正确的是

A

必拒绝 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>H</mi><mn>0</mn></msub></math>$

B

必接受 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>H</mi><mn>0</mn></msub></math>$

C

第一类错误的概率变大

D

可能接受，也可能拒绝 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>H</mi><mn>0</mn></msub></math>$

设 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>X</mi><mn>1</mn></msub><mo> </mo><mo>,</mo><mo> </mo><msub><mi>X</mi><mn>2</mn></msub><mo> </mo><mo>,</mo><mo>⋯</mo><mo>,</mo><mo> </mo><msub><mi>X</mi><mi>n</mi></msub><mfenced><mrow><mi>n</mi><mo>≥</mo><mn>2</mn></mrow></mfenced></math>$ 为取自总体 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>N</mi><mfenced><mrow><mn>0</mn><mo>,</mo><mn>1</mn></mrow></mfenced></math>$ 的简单随机样本，其样本均值 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>X</mi><mo>¯</mo></mover><mo>=</mo><mfrac><mn>1</mn><mi>n</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>X</mi><mi>i</mi></msub></math>$ ，样本方差 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>S</mi><mn>2</mn></msup><mo>=</mo><mfrac><mn>1</mn><mrow><mi>n</mi><mo>-</mo><mn>1</mn></mrow></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msup><mfenced><mrow><msub><mi>X</mi><mi>i</mi></msub><mo>-</mo><mover><mi>X</mi><mo>¯</mo></mover></mrow></mfenced><mn>2</mn></msup></math>$ ，则

A

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mover><mi>X</mi><mo>¯</mo></mover><mo>~</mo><mi>N</mi><mfenced><mrow><mn>0</mn><mo>,</mo><mn>1</mn></mrow></mfenced></math>$

B

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><msup><mi>S</mi><mn>2</mn></msup><mo>~</mo><msup><mi>χ</mi><mn>2</mn></msup><mfenced><mi>n</mi></mfenced></math>$

C

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><msqrt><mi>n</mi><mi>X</mi></msqrt><mi>S</mi></mfrac><mo>~</mo><mi>t</mi><mfenced><mrow><mi>n</mi><mo>-</mo><mn>1</mn></mrow></mfenced><mi></mi></math>$

D

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><msup><mover><mi>X</mi><mo>¯</mo></mover><mn>2</mn></msup><msup><mi>S</mi><mn>2</mn></msup></mfrac><mo>~</mo><mi>F</mi><mfenced><mrow><mn>1</mn><mo>,</mo><mi>n</mi><mo>-</mo><mn>1</mn></mrow></mfenced><mi></mi></math>$

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mfrac><mi>x</mi><mrow><mn>1</mn><mo>+</mo><msup><mi>x</mi><mn>2</mn></msup></mrow></mfrac></math>$ 的有界性为

A

在定义域 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>(</mo><mo>-</mo><mo>∞</mo><mo>,</mo><mn>0</mn><mo>)</mo></math>$ 上是有界的

B

在定义域 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>(</mo><mo>-</mo><mn>1</mn><mo>,</mo><mo>+</mo><mo>∞</mo><mo>)</mo></math>$ 上是有界的

C

在定义域 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>(</mo><mo>-</mo><mo>∞</mo><mo>,</mo><mo>+</mo><mo>∞</mo><mo>)</mo></math>$ 上是有界的

D

该函数在定义域内无界

填空题（每小题4分，数一同学完成：11、12、13、14、15、16题。数三同学完成：11、12、13、14、16、17题。）

已知两曲线 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>f</mi><mfenced><mi>x</mi></mfenced></math>$ 与 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><msubsup><mo>∫</mo><mn>0</mn><mrow><mi>a</mi><mi>r</mi><mi>c</mi><mi>tan</mi><mi>x</mi></mrow></msubsup><msup><mi>e</mi><mrow><mo>-</mo><msup><mi>t</mi><mn>2</mn></msup></mrow></msup><mi>d</mi><mi>t</mi></math>$ 在 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mrow><mn>0</mn><mo>,</mo><mn>0</mn></mrow></mfenced></math>$ 处的切线相互垂直，则 $<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mi>lim</mi><mrow><mi>n</mi><mo>→</mo><mo>∞</mo></mrow></munder><mi>n</mi><mi>f</mi><mfenced><mfrac><mn>2</mn><mi>n</mi></mfrac></mfenced><mo>=</mo><mi></mi></math>$ ______。

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>f</mi><mfenced><mi>x</mi></mfenced></math>$ 的反函数是 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>=</mo><mi>φ</mi><mfenced><mi>y</mi></mfenced></math>$ ，且 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><msubsup><mo>∫</mo><mn>1</mn><mrow><mn>2</mn><mi>x</mi></mrow></msubsup><msup><mi>e</mi><msup><mi>t</mi><mn>2</mn></msup></msup><mo>d</mo><mi>t</mi><mo>+</mo><mn>1</mn></math>$ ，则 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>φ</mi><mo>''</mo></msup><mfenced><mn>1</mn></mfenced><mo>=</mo></math>$ __________。

设 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mo> </mo><mi>y</mi></mrow></mfenced></math>$ 连续，且 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mo> </mo><mi>y</mi></mrow></mfenced><mo>=</mo><mi>x</mi><mi>y</mi><mo>+</mo><munder><mo>∬</mo><mi>D</mi></munder><mi>f</mi><mfenced><mrow><mi>u</mi><mo>,</mo><mi>v</mi></mrow></mfenced><mi>d</mi><mi>u</mi><mi>d</mi><mi>v</mi></math>$ ，其中D是由 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mn>0</mn><mo>,</mo><mi>y</mi><mo>=</mo><msup><mi>x</mi><mn>2</mn></msup><mo>,</mo><mi>x</mi><mo>=</mo><mn>1</mn></math>$ 所围成的区域，则 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mo> </mo><mi>y</mi></mrow></mfenced><mo>=</mo></math>$ __________。

若函数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>z</mi><mo>=</mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mo> </mo><mi>y</mi></mrow></mfenced></math>$ 满足 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>z</mi></mrow><mrow><mo>∂</mo><msup><mi>y</mi><mn>2</mn></msup></mrow></mfrac><mo>=</mo><mn>2</mn><mi></mi></math>$ ，且 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mn>1</mn></mrow></mfenced><mo>=</mo><mi>x</mi><mo>+</mo><mn>2</mn></math>$ ，又 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>f</mi><mi>y</mi><mo>'</mo></msubsup><mfenced><mrow><mi>x</mi><mo>,</mo><mn>1</mn></mrow></mfenced><mo>=</mo><mi>x</mi><mo>+</mo><mn>1</mn></math>$ ，则 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mo> </mo><mi>y</mi></mrow></mfenced><mo>=</mo></math>$ __________。

从 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>R</mi><mn>2</mn></msup></math>$ 的基 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>α</mi><mn>1</mn></msub><mo>=</mo><mfenced><mtable><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd></mtr></mtable></mfenced><mo>,</mo><msub><mi>α</mi><mn>2</mn></msub><mo>=</mo><mfenced><mtable><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>1</mn></mtd></mtr></mtable></mfenced></math>$ 到基 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>β</mi><mn>1</mn></msub><mo>=</mo><mfenced><mtable><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr></mtable></mfenced><mo>,</mo><msub><mi>β</mi><mn>2</mn></msub><mo>=</mo><mfenced><mtable><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>2</mn></mtd></mtr></mtable></mfenced></math>$ 的过渡矩阵为__________。

设随机变量X和Y分别服从二项分布 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mfenced><mrow><mn>2</mn><mo>,</mo><mo> </mo><mi>p</mi></mrow></mfenced></math>$ 和 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mfenced><mrow><mn>3</mn><mo>,</mo><mo> </mo><mi>p</mi></mrow></mfenced></math>$ 。若 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi><mfenced open="{" close="}"><mrow><mi>X</mi><mo>≥</mo><mn>1</mn></mrow></mfenced><mo>=</mo><mfrac><mn>5</mn><mn>9</mn></mfrac></math>$ ，则 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi><mfenced open="{" close="}"><mrow><mi>Y</mi><mo>≥</mo><mi>E</mi><mi>Y</mi></mrow></mfenced><mo>=</mo></math>$ ________。

设 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi><mo>,</mo><mi>β</mi><mo>,</mo><mi>γ</mi></math>$ 是3维列向量，已知 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="|" close="|"><mi>B</mi></mfenced><mo>=</mo><mfenced open="|" close="|"><mrow><mn>2</mn><mi>α</mi><mo>-</mo><mi>β</mi><mo>,</mo><mn>2</mn><mi>β</mi><mo>-</mo><mi>γ</mi><mo>,</mo><mn>2</mn><mi>γ</mi><mo>-</mo><mi>α</mi></mrow></mfenced><mo>=</mo><mi>a</mi><mi></mi></math>$ ，则 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="|" close="|"><mi>A</mi></mfenced><mo>=</mo><mfenced open="|" close="|"><mrow><mi>α</mi><mo>,</mo><mi>β</mi><mo>,</mo><mi>γ</mi></mrow></mfenced><mo>=</mo><mi></mi></math>$ ________。

简答题（数一同学完成：18、19、20、21、22、23、24、25、26题。数三同学完成：23、25、26、27、28、29、30、31、32题。）

$<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mi>lim</mi><mrow><mi>x</mi><mo>→</mo><msup><mn>0</mn><mo>+</mo></msup></mrow></munder><mfenced><mrow><mfrac><mn>1</mn><mrow><mi>ln</mi><mfenced><mrow><mi>x</mi><mo>+</mo><msqrt><mn>1</mn><mo>+</mo><msup><mi>x</mi><mn>2</mn></msup></msqrt></mrow></mfenced></mrow></mfrac><mo>-</mo><mfrac><mn>1</mn><mrow><mi>ln</mi><mstyle displaystyle="true"><mfenced><mrow><mn>1</mn><mo>+</mo><mi>x</mi></mrow></mfenced></mstyle></mrow></mfrac></mrow></mfenced><mi></mi></math>$

$<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mi>y</mi></mrow></mfenced><mo>=</mo><mfenced open="{" close=""><mtable columnalign="left"><mtr><mtd><mi>x</mi><mi>y</mi><mfrac><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><msup><mi>y</mi><mn>2</mn></msup></mrow><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup></mrow></mfrac><mo>,</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>≠</mo><mn>0</mn></mtd></mtr><mtr><mtd><mn>0</mn><mo>,</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>=</mo><mn>0</mn></mtd></mtr></mtable></mfenced></math>$
求：（Ⅰ） $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo>=</mo><msubsup><mi>f</mi><mrow><mi>x</mi><mi>y</mi></mrow><mo>''</mo></msubsup><mfenced><mrow><mn>0</mn><mo>,</mo><mn>0</mn></mrow></mfenced></math>$ 和 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi><mo>=</mo><msubsup><mi>f</mi><mrow><mi>y</mi><mi>x</mi></mrow><mo>''</mo></msubsup><mfenced><mrow><mn>0</mn><mo>,</mo><mn>0</mn></mrow></mfenced></math>$ ；
（Ⅱ）满足 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>'</mo><mfenced><mi>x</mi></mfenced><mo>+</mo><msup><mi>x</mi><mn>2</mn></msup><mi>y</mi><mo>'</mo><mfenced><mrow><mo>-</mo><mi>x</mi></mrow></mfenced><mo>=</mo><mi>k</mi></math>$ ，及 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mfenced><mn>0</mn></mfenced><mo>=</mo><mi>a</mi></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mi>lim</mi><mrow><mi>x</mi><mo>→</mo><mo>+</mo><mo>∞</mo></mrow></munder><mi>y</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mi>b</mi></math>$ 的函数和表达式。

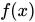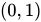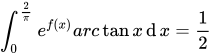设函数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced></math>$ 在闭区间 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="[" close="]"><mrow><mn>0</mn><mo>,</mo><mn>1</mn></mrow></mfenced></math>$ 上连续，在开区间 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mrow><mn>0</mn><mo>,</mo><mn>1</mn></mrow></mfenced></math>$ 内可导，且有 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mo>∫</mo><mn>0</mn><mfrac><mn>2</mn><mi mathvariant="normal">π</mi></mfrac></msubsup><msup><mi>e</mi><mrow><mi>f</mi><mfenced><mi>x</mi></mfenced></mrow></msup><mi>a</mi><mi>r</mi><mi>c</mi><mi>tan</mi><mi>x</mi><mo>d</mo><mi>x</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi></mi></math>$ ， $<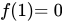math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mn>1</mn></mfenced><mo>=</mo><mn>0</mn></math>$ ，证明至少存在一点 $<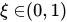math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ξ</mi><mo>∈</mo><mfenced><mrow><mn>0</mn><mo>,</mo><mn>1</mn></mrow></mfenced></math>$ ，使得 $<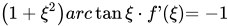math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mrow><mn>1</mn><mo>+</mo><msup><mi>ξ</mi><mn>2</mn></msup></mrow></mfenced><mi>a</mi><mi>r</mi><mi>c</mi><mi>tan</mi><mi>ξ</mi><mo>·</mo><mi>f</mi><mo>'</mo><mfenced><mi>ξ</mi></mfenced><mo>=</mo><mo>-</mo><mn>1</mn></math>$ 。

计算 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>I</mi><mo>=</mo><munder><mo>∮</mo><mi>Γ</mi></munder><mfenced><mrow><mo>-</mo><msup><mi>y</mi><mn>2</mn></msup></mrow></mfenced><mi>d</mi><mi>x</mi><mo>+</mo><mi>x</mi><mi>d</mi><mi>y</mi><mo>+</mo><msup><mi>z</mi><mn>2</mn></msup><mi>d</mi><mi>z</mi></math>$ ，其中 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Γ</mi></math>$ 是平面 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>+</mo><mi>z</mi><mo>=</mo><mn>2</mn></math>$ ，与柱面 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>=</mo><mn>1</mn></math>$ 的交线，从 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>z</mi></math>$ 轴正向看去， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Γ</mi></math>$ 取逆时针方向。

求幂级数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><munderover><mo>∑</mo><mrow><mi>n</mi><mo>=</mo><mn>1</mn></mrow><mo>∞</mo></munderover><mfrac><mrow><msup><mfenced><mrow><mo>-</mo><mn>1</mn></mrow></mfenced><mrow><mi>n</mi><mo>-</mo><mn>1</mn></mrow></msup><msup><mi>x</mi><mrow><mn>2</mn><mi>n</mi><mo>+</mo><mn>1</mn></mrow></msup></mrow><mrow><mi>n</mi><mfenced><mrow><mn>2</mn><mi>n</mi><mo>-</mo><mn>1</mn></mrow></mfenced></mrow></mfrac><mi></mi></math>$ 的收敛域及和函数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>S</mi><mfenced><mi>x</mi></mfenced></math>$ 。

已知 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo>=</mo><mfenced><mrow><msub><mi>α</mi><mn>1</mn></msub><mo>,</mo><msub><mi>α</mi><mn>2</mn></msub><mo>,</mo><msub><mi>α</mi><mn>3</mn></msub><mo>,</mo><msub><mi>α</mi><mn>4</mn></msub></mrow></mfenced></math>$ 为4阶方阵， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>x</mi><mo>=</mo><mi>β</mi></math>$ 的通解为 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>2</mn></mtd></mtr><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>1</mn></mtd></mtr></mtable></mfenced><mo>+</mo><mi>k</mi><mfenced open="[" close="]"><mtable><mtr><mtd><mn>1</mn></mtd></mtr><mtr><mtd><mn>3</mn></mtd></mtr><mtr><mtd><mn>2</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd></mtr></mtable></mfenced><mi></mi></math>$ ，其中 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mo>=</mo><mfenced><mrow><msub><mi>α</mi><mn>3</mn></msub><mo>,</mo><msub><mi>α</mi><mn>2</mn></msub><mo>,</mo><msub><mi>α</mi><mn>1</mn></msub><mo>,</mo><mi>β</mi><mo>+</mo><msub><mi>α</mi><mn>4</mn></msub></mrow></mfenced></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>γ</mi><mo>=</mo><msub><mi>α</mi><mn>1</mn></msub><mo>-</mo><mn>3</mn><msub><mi>α</mi><mn>2</mn></msub><mo>+</mo><mn>5</mn><msub><mi>α</mi><mn>3</mn></msub></math>$ ，求：
（Ⅰ） $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>α</mi><mn>1</mn></msub></math>$ 能否由 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>α</mi><mn>2</mn></msub><mo>,</mo><msub><mi>α</mi><mn>3</mn></msub></math>$ 线性表示；
（Ⅱ） $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>α</mi><mn>4</mn></msub></math>$ 能否由 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>α</mi><mn>1</mn></msub><mo>,</mo><msub><mi>α</mi><mn>2</mn></msub><mo>,</mo><msub><mi>α</mi><mn>3</mn></msub></math>$ 线性表示；
（Ⅲ）求 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mi>x</mi><mo>=</mo><mi>γ</mi></math>$ 的通解。

设3维向量空间有两个基 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>e</mi><mn>1</mn></msub><mo>,</mo><msub><mi>e</mi><mn>2</mn></msub><mo>,</mo><msub><mi>e</mi><mn>3</mn></msub></math>$ 和 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>e</mi><mn>1</mn><mo>'</mo></msubsup><mo>,</mo><msubsup><mi>e</mi><mn>2</mn><mo>'</mo></msubsup><mo>,</mo><msubsup><mi>e</mi><mn>3</mn><mo>'</mo></msubsup></math>$ ，它们满足 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced open="{" close=""><mtable columnalign="left"><mtr><mtd><msubsup><mi>e</mi><mn>1</mn><mo>'</mo></msubsup><mo>=</mo><msub><mi>e</mi><mn>1</mn></msub><mo>-</mo><msub><mi>e</mi><mn>2</mn></msub></mtd></mtr><mtr><mtd><msubsup><mi>e</mi><mn>2</mn><mo>'</mo></msubsup><mo>=</mo><mn>2</mn><msub><mi>e</mi><mn>1</mn></msub><mo>+</mo><mn>3</mn><msub><mi>e</mi><mn>2</mn></msub><mo>+</mo><mn>2</mn><msub><mi>e</mi><mn>3</mn></msub></mtd></mtr><mtr><mtd><msubsup><mi>e</mi><mn>3</mn><mo>'</mo></msubsup><mo>=</mo><msub><mi>e</mi><mn>1</mn></msub><mo>+</mo><mn>3</mn><msub><mi>e</mi><mn>2</mn></msub><mo>+</mo><mn>2</mn><msub><mi>e</mi><mn>3</mn></msub></mtd></mtr></mtable></mfenced></math>$
如果向量 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi><mo>=</mo><mn>2</mn><msub><mi>e</mi><mn>1</mn></msub><mo>-</mo><msub><mi>e</mi><mn>2</mn></msub><mo>+</mo><mn>3</mn><msub><mi>e</mi><mn>3</mn></msub></math>$ ，在基 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msubsup><mi>e</mi><mn>1</mn><mo>'</mo></msubsup><mo>,</mo><msubsup><mi>e</mi><mn>2</mn><mo>'</mo></msubsup><mo>,</mo><msubsup><mi>e</mi><mn>3</mn><mo>'</mo></msubsup></math>$ 下的坐标 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>x</mi><mn>1</mn></msub><mo>,</mo><msub><mi>x</mi><mn>2</mn></msub><mo>,</mo><msub><mi>x</mi><mn>3</mn></msub></math>$ 组成的3维向量 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ξ</mi><mo>=</mo><msup><mfenced><mrow><msub><mi>x</mi><mn>1</mn></msub><mo>,</mo><msub><mi>x</mi><mn>2</mn></msub><mo>,</mo><msub><mi>x</mi><mn>3</mn></msub></mrow></mfenced><mi>T</mi></msup></math>$ 是3阶矩阵 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo>=</mo><mfenced open="[" close="]"><mtable><mtr><mtd><mn>2</mn></mtd><mtd><mn>0</mn></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mo>-</mo><mn>2</mn></mtd><mtd><mi>a</mi></mtd><mtd><mn>0</mn></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mi>b</mi></mtd><mtd><mn>2</mn></mtd></mtr></mtable></mfenced></math>$ 的一个特征向量。
（Ⅰ）求常数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo>,</mo><mi>b</mi></math>$ ；
（Ⅱ）问 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>$ 能否与对角阵相似？如果能，求使得 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>P</mi><mrow><mo>-</mo><mn>1</mn></mrow></msup><mi>A</mi><mi>P</mi><mo>=</mo><mi>Λ</mi></math>$ 的可逆矩阵和对角矩阵 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Λ</mi></math>$ ；如果不能，说明理由。

设随机变量 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>X</mi></math>$ 与 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Y</mi></math>$ 相互独立， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>X</mi></math>$ 服从 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>p</mi><mo>=</mo><mfrac><mn>3</mn><mn>5</mn></mfrac></math>$ 的 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mo>-</mo><mn>1</mn></math>$ 分布， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Y</mi></math>$ 的概率分布律为 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi><mfenced open="{" close="}"><mrow><mi>Y</mi><mo>=</mo><mi>i</mi></mrow></mfenced><mo>=</mo><mfrac><mn>1</mn><mn>3</mn></mfrac><mo>,</mo><mfenced><mrow><mi>i</mi><mo>=</mo><mo>-</mo><mn>1</mn><mo>,</mo><mn>0</mn><mo>,</mo><mn>1</mn></mrow></mfenced></math>$ ；记 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Z</mi><mo>=</mo><mi>X</mi><mo>-</mo><mi>Y</mi></math>$ 。
（Ⅰ）求 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi><mfenced open="{" close="}"><mrow><menclose notation="right"><mi>X</mi><mo>=</mo><mn>0</mn></menclose><mi>Z</mi><mo>=</mo><mn>0</mn></mrow></mfenced></math>$ ；
（Ⅱ）求二维随机变量 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mrow><mi>X</mi><mo>,</mo><mi>Y</mi></mrow></mfenced></math>$ 的概率分布律；
（Ⅲ）求 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Z</mi></math>$ 的方差 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mfenced><mi>Z</mi></mfenced></math>$ 。

设总体 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>X</mi></math>$ 的概率密度为 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mi>θ</mi></mrow></mfenced><mo>=</mo><mfenced open="{" close=""><mtable columnalign="left"><mtr><mtd><mi>θ</mi><msup><mi>e</mi><mrow><mo>-</mo><mi>θ</mi><mi>x</mi></mrow></msup><mo>,</mo><mi>x</mi><mo>></mo><mn>0</mn></mtd></mtr><mtr><mtd><mn>0</mn><mo>,</mo><mi>x</mi><mo>≤</mo><mn>0</mn></mtd></mtr></mtable></mfenced></math>$ ，其中参数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi><mfenced><mrow><mn>0</mn><mo><</mo><mi>θ</mi><mo><</mo><mn>1</mn></mrow></mfenced></math>$ 未知， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>X</mi><mn>1</mn></msub><mo>,</mo><msub><mi>X</mi><mn>2</mn></msub><mo>,</mo><mo>⋯</mo><mo>,</mo><msub><mi>X</mi><mi>n</mi></msub></math>$ 是来自总体 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>X</mi></math>$ 的简单随机样本， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>X</mi><mo>¯</mo></mover></math>$ 为样本的样本均值。
（Ⅰ）求参数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi></math>$ 的矩估计量 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mover><mi>θ</mi><mo>^</mo></mover><mn>1</mn></msub></math>$ ；
（Ⅱ）求参数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>θ</mi></math>$ 的最大似然估计量 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mover><mi>θ</mi><mo>^</mo></mover><mn>2</mn></msub></math>$ 。

已知三元二次型 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>x</mi><mi>T</mi></msup><mi>A</mi><mi>x</mi></math>$ 经正交变换为 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><msubsup><mi>y</mi><mn>1</mn><mn>2</mn></msubsup><mo>-</mo><msubsup><mi>y</mi><mn>2</mn><mn>2</mn></msubsup><mo>-</mo><msubsup><mi>y</mi><mn>3</mn><mn>2</mn></msubsup></math>$ ，又知 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>$ 满足矩阵方程 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mfenced open="[" close="]"><msup><mfenced><mrow><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>A</mi></mrow></mfenced><mo></mo></msup></mfenced><mrow><mo>-</mo><mn>1</mn></mrow></msup><mi>B</mi><msup><mi>A</mi><mrow><mo>-</mo><mn>1</mn></mrow></msup></math>$ $<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>=</mo><mn>2</mn><mi>A</mi><mi>B</mi><mo>+</mo><mn>4</mn><mi>E</mi></math>$ ，且 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo></mo><mi>α</mi><mo>=</mo><mi>α</mi></math>$ ，其中 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi><mo>=</mo><msup><mfenced><mrow><mn>1</mn><mo>,</mo><mn>1</mn><mo>,</mo><mo>-</mo><mn>1</mn></mrow></mfenced><mi>T</mi></msup></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo>*</mo></math>$ 为 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>$ 的伴随矩阵，求次二次型 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>x</mi><mi>T</mi></msup><mi>B</mi><mi>x</mi></math>$ 的表达式。

已知一抛物线通过x轴上的两点 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mo> </mo><mi>A</mi><mfenced><mrow><mn>1</mn><mo>,</mo><mn>0</mn></mrow></mfenced><mo>,</mo><mi>B</mi><mfenced><mrow><mn>3</mn><mo>,</mo><mn>0</mn></mrow></mfenced></math>$ 。
（Ⅰ）求证两坐标轴与该抛物线所围成图形的面积等于 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>O</mi><mi>x</mi></math>$ 轴与该抛物线所围图形的面积；
（Ⅱ）计算上述两平面图形绕 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>O</mi><mi>x</mi></math>$ 轴旋转一周所产生的两旋转体体积之比。

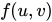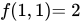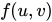已知 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>u</mi><mo>,</mo><mi>v</mi></mrow></mfenced></math>$ 具有连续的二阶偏导数， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mn>1</mn><mo>,</mo><mn>1</mn></mrow></mfenced><mo>=</mo><mn>2</mn></math>$ 是 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mrow><mi>u</mi><mo>,</mo><mi>v</mi></mrow></mfenced></math>$ 的极值， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>z</mi><mo>=</mo><mi>f</mi><mfenced open="[" close="]"><mrow><mi>x</mi><mo>+</mo><mi>y</mi><mo>,</mo><mo> </mo><mi>f</mi><mfenced><mrow><mi>x</mi><mo>,</mo><mo> </mo><mi>y</mi></mrow></mfenced></mrow></mfenced></math>$ ，求 $<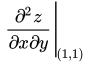math xmlns="http://www.w3.org/1998/Math/MathML"><msub><menclose notation="right"><mfrac><mrow><msup><mo>∂</mo><mn>2</mn></msup><mi>z</mi></mrow><mrow><mo>∂</mo><mi>x</mi><mo>∂</mo><mi>y</mi></mrow></mfrac></menclose><mfenced><mrow><mn>1</mn><mo>,</mo><mn>1</mn></mrow></mfenced></msub><mi></mi></math>$ 。

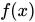若函数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>x</mi></mfenced></math>$ 在 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mrow><mo>-</mo><mo>∞</mo><mo>,</mo><mo>+</mo><mo>∞</mo></mrow></mfenced><mi></mi></math>$ 内可导，又 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mfenced><mi>a</mi></mfenced><mo>=</mo><mi>f</mi><mfenced><mi>b</mi></mfenced><mo>=</mo><mn>0</mn><mi></mi></math>$ ，且 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>f</mi><mo>'</mo></msup><mfenced><mi>a</mi></mfenced><mo><</mo><mn>0</mn></math>$ ， $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>f</mi><mo>'</mo></msup><mfenced><mi>b</mi></mfenced><mo><</mo><mn>0</mn></math>$ 试证 $<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mi>f</mi><mo>'</mo></msup><mfenced><mi>x</mi></mfenced></math>$ 在 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mrow><mi>a</mi><mo>,</mo><mi>b</mi></mrow></mfenced></math>$ 内至少有两个不同的实根。

设某产品的成本函数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mo>=</mo><mi>a</mi><msup><mi>q</mi><mn>2</mn></msup><mo>+</mo><mi>b</mi><mi>q</mi><mo>+</mo><mi>c</mi></math>$ ，需求函数 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>q</mi><mo>=</mo><mfrac><mn>1</mn><mi>e</mi></mfrac><mfenced><mrow><mi>d</mi><mo>-</mo><mi>P</mi></mrow></mfenced></math>$ ，其中 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>$ 为成本， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>q</mi></math>$ 为需求量（即产量）， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi></math>$ 为单位价格， $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>,</mo><mi>d</mi><mo>,</mo><mi>e</mi></math>$ 都是正的常数，且 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi><mo>></mo><mi>b</mi></math>$ 求：
（Ⅰ）利润最大时的产量及最大利润；
（Ⅱ）需求对价格的弹性 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>η</mi><mfenced><mrow><mi>η</mi><mo>></mo><mn>0</mn></mrow></mfenced></math>$ ；
（Ⅲ）需求对价格弹性的绝对值为 $<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>$ 时的产量。

$<math xmlns="http://www.w3.org/1998/Math/MathML"><munder><mi>lim</mi><mrow><mi>x</mi><mo>→</mo><mn>1</mn></mrow></munder><mfrac><mrow><msup><mi>x</mi><mi>x</mi></msup><mo>-</mo><mi>x</mi></mrow><mrow><mi>ln</mi><mi>x</mi><mo>-</mo><mi>x</mi><mo>+</mo><mn>1</mn></mrow></mfrac><mi></mi></math>$

已答未答

单选题（每小题4分，数一同学完成：1、2、3、4、5、6、7、8题。数三同学完成：1、2、3、5、6、7、9、10题。）（总分40分，共10题）

填空题（每小题4分，数一同学完成：11、12、13、14、15、16题。数三同学完成：11、12、13、14、16、17题。）（总分28分，共7题）

简答题（数一同学完成：18、19、20、21、22、23、24、25、26题。数三同学完成：23、25、26、27、28、29、30、31、32题。）（总分155分，共15题）